Further refinement can be made to the probability of development obstacles.
Life depends on q planetary conditions.
That is, they form the set Q of obstacles to development.
Then each element contributes to the overall probability. This part is:
| 7.1.1 Equation |
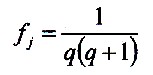 |
Es ist: 0 <
j < q + 1
Es gilt dann für die It then applies to the overall probability of development obstaclese:
| 7.1.2 Equation |
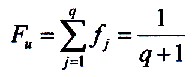 |
A differentiation of the individual components is achieved by weighting the individual elements.
| 7.1.3 Equation |
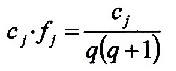 |
Then the probability of development obstacles results:
| 7.1.4 Equation |
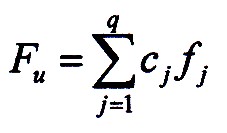 |
Overall, the likelihood of development obstacles is as follows:
| 7.1.5 Equation |
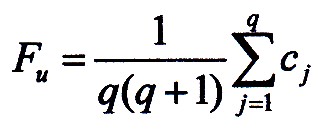 |
Equation
7.1.5 is the most general approach that can be made for an arbitrary set
Q of development obstacles, that can still be weighted in their influence by the cj
In a first approach it is assumed that all parts
have the same effect, so that the weighting factors are all one,
so Equation 7.1.2 applies.
| 7.1.6 Approach |
The weighting factors are set equal to one
c1
= c2
= ... = cj
= ... = cn
= 1 |
Here are 5 components that represent obstacles to development.
The following applies to the individual probability: fj = 1:30
Therefore, 5 failures can also occur.
SThe chance of development occurring is therefore 1 in 6.
This corresponds to a share of 16,66%.
The probability factor for development is therefore Fu = 0.166... = 1:6.
This approach is used as the basis for the calculations in all following considerations.
|